|
El Super Bowl es uno de los eventos deportivos de mayor audiencia del mundo y por tanto hay una enorme expectativa por conocer el ganador. Todos tienen su favorito y en esta edición el ganador se definirá entre Los Angeles Rams y New England Patriots. Existen todo tipo de métodos para pronosticar al ganador de un deporte, desde la mera corazonada, hasta sofisticados modelos estadísticos, aunque la cantidad de variables implicadas hace virtualmente imposible predecir con certeza un resultado.
La econometría es particularmente útil para encontrar las variables que explican un comportamiento consistente en el largo plazo. De esta forma, utilizando sólo estadísticas de los resultados en la temporada regular de la NFL, en los últimos diez años es posible construir un “modelo estadístico de elección binaria” con el cual se asocia cada equipo con una probabilidad de ganar el Super Bowl. De esta forma, realizamos un ejercicio con un modelo con las variables previamente elegidas mediante un algoritmo de selección. Así se conservan sólo las variables que sean capaces de explicar a los ganadores del Super Bowl. El resultado es que las variables que más aumentan la probabilidad de ganar el campeonato son las intercepciones totales (INT), capturas de mariscal de campo (SCK) y los touchdowns tras intercepciones (TD). Todas estas son estadísticas asociadas al desempeño de la defensa. |
Comparando las variables de mayor poder predictivo vemos que la diferencia entre Rams y Patriots sólo es en la cantidad de capturas de mariscal de campo, pues en los otros dos indicadores se encuentran empatados.
Estadísticas seleccionadas de temporada 2018
|
|
Intercepciones |
Capturas de mariscal |
TD tras intercepción |
|
Rams |
18 |
41 |
1 |
|
Patriots |
18 |
30 |
1 |
|
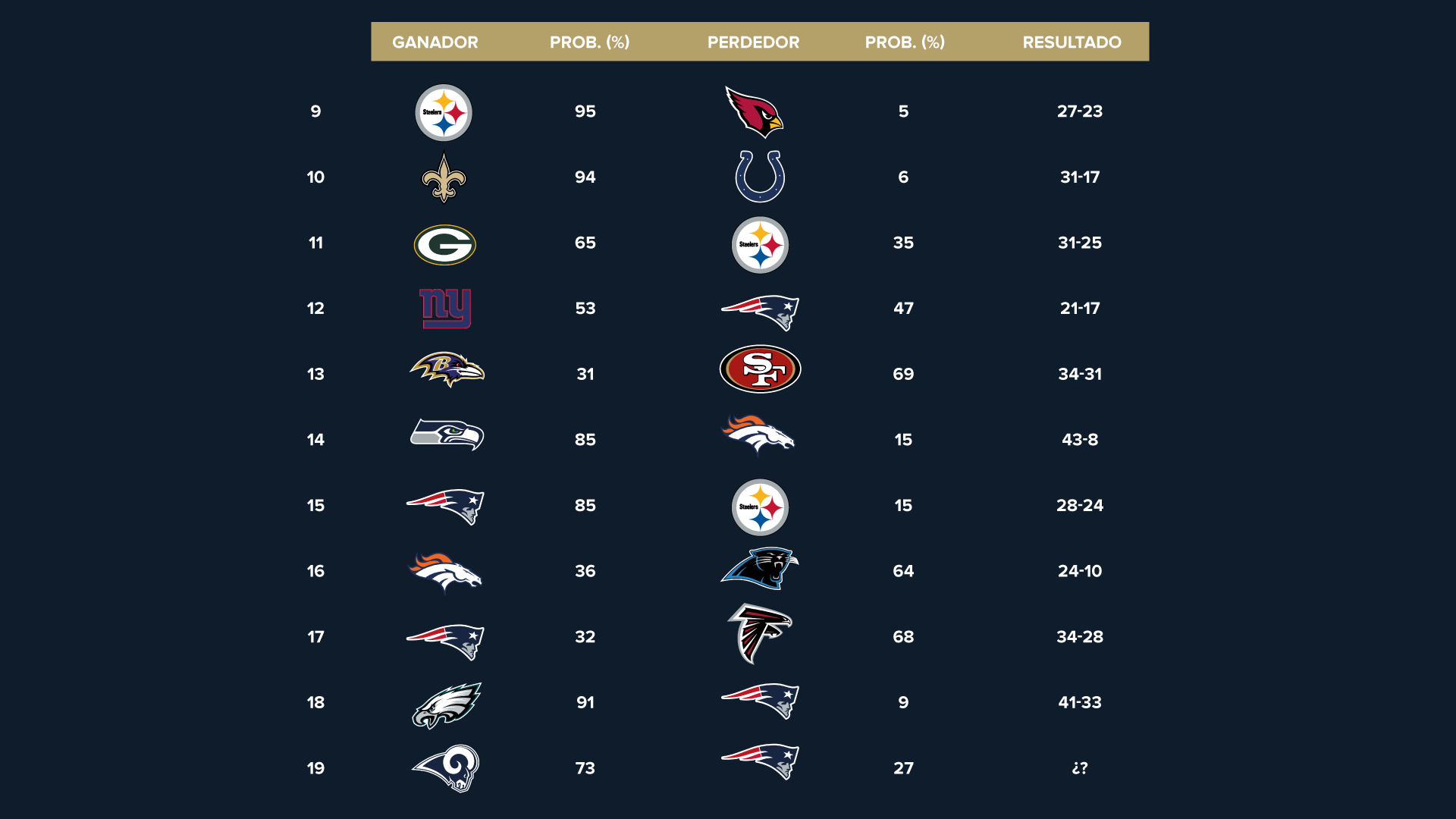
Con estos datos, el ganador esperado por el modelo, con una probabilidad de 73%, es el equipo de Los Angeles Rams. Históricamente, el modelo asigna una probabilidad más alta al finalista ganador en 7 de 10 ocasiones (tabla 1). |
Dicen que las defensas ganan campeonatos, la econometría parece estar de acuerdo. Veamos qué dice Tom Brady al respecto el próximo domingo.
Probabilidad asignada por el modelo para cada Super Bowl
|
Variable dependiente: SUPERBOWL |
|||||
|
Método: ML |
Binary Probit |
|
|||
|
Muestra: 2008 2017 |
|
|
|||
|
Observaciones: 320 |
|
|
|||
|
Obs con dep=0 |
310 |
|
|
||
|
Obs con dep=1 |
10 |
|
|
||
|
Variable |
Coeficiente |
Error estándar |
Significancia |
||
|
C |
-5.02 |
1.030691 |
*** |
||
|
INT |
0.078 |
0.032539 |
** |
||
|
SCK |
0.045 |
0.020504 |
** |
||
|
TD |
0.166 |
0.144594 |
. |
||
|
(***) 0.01 (**)0.05 (*)0.10 (.)>0.10 |
|
||||
|
Pseudo R^2 McFadden |
0.18 |
|
|
||

